Catatan Metode Penelitian #4

Pada catatan ini saya akan menjelaskan catatan metode penelitian yang dijelaskan oleh dosen saya, Pak Arry, terkait hipotesis, perumusan dan pengujiannya. 

Hipotesis berasal dari kata hupo dan thesis. Hupo artinya sementara/lemah kebenarannya dan thesis artinya pernyataan atau teori. Oleh karena itu, hipotesis merupakan jawaban sementara terhadap masalah penelitian yang kebenarannya harus diuji secara empiris. Adanya hipotesis dapat memberikan manfaat antara lain:

1. Memberikan batasan serta memperkecil jangkauan penelitian dan kerja penelitian.
2. Mempersiapkan peneliti pada kondisi fakta dan hubungan antar fakta yang kadang kala hilang dari perhatian peneliti.
3. Sebagai alat sederhana dalam memfokuskan fakta yang tersebar tanpa koordinasi.
4. Sebagai panduan pengujian.

Tinggi atau rendahnya manfaat hipotesis tergantung pada pengamatan yang tajam peneliti, imajinasi serta pemikiran kreatif peneliti, kerangka analisis yang digunakan peneliti, dan metode serta disain yang digunakan peneliti.

Ciri-ciri dari hipotesis antara lain:

1. Harus menyatakan hubungan;
2. Harus sesuai dengan fakta;
3. Berhubungan dengan ilmu;
4. Harus dapat diuji;
5. Harus sederhana;
6. Harus bisa menerangkan fakta.

Jenis hipotesis antara lain:

1. Hipotesis hubungan dan perbedaan;
2. Hipotesis kerja dan hipotesis nul;
3. Hipotesis common sense dan ideal.

Dalam menggali dan merumuskan hipotesis, peneliti harus mempunyai banyak informasi tentang masalah yang ingin dipecahkan, mempunyai kemampuan memeriksa informasi tentang objek-objek yang berhubungan dalam fenomena yang diselidiki, dan mempunyai kemampuan menghubungkan suatu keadaan dengan keadaan lain dengan kerangka teori dan bidang yang bersangkutan.

Sumber hipotesis menurut Goode dan Hatt (1952) antara lain:

1. Kebudayaan di aman ilmu tersebut dibentuk; 
2. Ilmu itu sendiri yang memberikan teori dan teori memberikan arah pada penelitian;
3. Analogi; 
4. Reaksi individu dan pengalaman;
5. Ilmu pengetahuan dan pengertian mendalam tentang ilmu;
6. Wawasan;
7. Imajinasi dan angan-angan;
8. Materi bacaan atau literatur;
9. Pengetahuan tentang kebiasaan atau kegiatan di suatu tempat;
10. Data yang tersedia.

Perumusan hipotesis bukanlah hal yang mudah. Penyebab kesulitan perumusan hipotesis antara lain:

1. Tak ada kerangka teori atau tak ada pengetahuan tentang kerangka teori yang jelas;
2. Kurang kemampuan untuk menggunakan kerangka teori yang ada;
3. Gagal berkenalan dengan teknik-teknik yang ada untuk merangkaikan kata-kata dalam membuat hipotesis dengan benar.

Beberapa hal yang perlu diperhatikan dalam perumusan hipotesis, yaitu:

1. Dinyatakan sebagai kalimat pernyataan (deklaratif)
2. Melibatkan minibal dua variabel penelitian
3. Mengandung suatu prediksi
4. Harus dapat diuji (testable)

Selain jenis hipotesis yang sudah disebutkan sebelumnya, terdapat dua hipotesis yang paling umum diketahui yaitu hipotesis korelatif dan hipotesis komparatif. Hipotesis korelatif merupakan pernyatan tentang ada atau tidaknya hubungan antara dua variabel atau lebih. Sementara hipotesis komparatif yaitu pernyataan tentang ada atau tidaknya perbedaan antara dua kelompok atau lebih.

Dalam hal ini, dikenal pula dua tipe hipotesis yaitu hipotesis nihil/nol (H0) dan hipotesis alternatif (Ha). H0 merupakan hipotesis yang menyatakan tidak adanya hubungan antara dua variabel atau lebih atau tidak adanya perbedaan antara dua kelompok atau lebih. Sementara hipotesis alternatif merupakan hipotesis yang menyatakan adanya hubungan antara dua variabel atau lebih atau adanya perbedaan antara dua kelompok atau lebih. 

Setelah hipotesis dirumuskan, selanjutnya hipotesis dilakukan pengujian. Pengujian hipotesis dapat berguna untuk membantu mengambil keputusan tentang apakah suatu hipotesis yang diajukan seperti perbedaan atau hubungan cukup meyakinkan untuk ditolak atau tidak ditolak. Keyakinan ini didasarkan pada besarnya peluang untuk memperoleh hubungan tersebut  secara kebetulan (by chance). Semakin kecilnya peluar tersebut (peluang adanya by chance) maka semakin besar keyakinan bahwa hubungan tersebut memang ada. 

Kesimpulan yang didapatkan dari hasil pengujian hipotesis ada dua kemungkinan, yaitu menolak hipotesis atau menerima hipotesis (gagal menolak hipotesis). Dalam hal ini, sebenarnya, menerima hipotesis bukan merupakan kesimpulan yang tepat, kesimpulan yang tepat yang dapat digunakan adalah gagal menolak hipotesis. Misalnya tetap menggunakan kesimpulan menerima hipotesis, maka kita menyimpulkan bahwa hipotesis tersebut benar, padahal benar atau tidaknya suatu hipotesis hanya dapat dibuktikan dengan mengadakan observasi mendalam pada seluruh populasi yang dalam hal ini sulit bahkan tidak mungkin untuk dilakukan.

Contoh yang lebih konkretnya, misalnya dalam suatu persidangan, kegagalan membuktikan kesalahan si tertuduh bukan berarti si tertuduh tidak bersalah atau si tertuduh benar. Pengadilan memutuskan bahwa si tertuduh tidak dapat dibuktikan bersalah bukan memutuskan tidak bersalah. Dari uraian tersebut jelas bahwa istilah yang tetap dalam kesimpulan uji hipotesis adalah gagal menolak hipotesis dan bukan menerima hipotesis. 

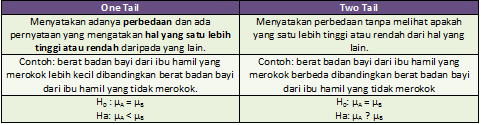
Dalam pengujian hipotesis menggunakan statistik, dikenal yang namanya arah atau bentuk uji hipotesis, yang terdiri dari one tail (satu sisi) dan two tail (dua sisi). Perbedaannya dapat dilihat pada tabel di bawah ini.

Berikut merupakan perbedaan antara one tail dan two tail dilihat dari grafiknya.

Dalam hal ini, terdapat suatu kesalahan dalam pengambilan keputusan. Ada dua jenis kesalahan dalam pengambilan keputusan dalam uji statistik yaitu kesalahan tipe I (α) dan kesalahan tipe II (b). 

Kesimpulan benar apabila fakta benar (tidak ada perbedaan) maka hipotesis diterima, kekeliruan dapat terjadi apabila faktanya salah (ada perbedaan) namun hipotesis tetap diterima. Kesimpulan yang lain terjadi dengan benar apabila fakta salah (ada perbedaan) sehingga hipotesis ditolak, kekeliruan terjadi jika faktanya ternyata benar (tidak ada perbedaan), tetapi hipotesis ditolak. 

Kesalahan atau kekeliruan tipe II merupakan kesalahan tidak menolak Ho padahal sesungguhnya Ho salah. Artinya menyimpulkan tidak ada perbedaan padahal sesungguhnya ada perbedaan. Peluangnya untuk membuat kesalahan tipe II ini sebesar b. Artinya, peluang untuk tidak membuat kesalahan tipe II adalah sebesar 1- b yang dikenal sebagai Tingkat Kekuatan Uji (Power of the test).

Dalam pengujian hipotesis dikehendaki nilaiα dan b kecil atau (1-α) dan (1-b) besar. Namun hal ini sulit dicapai karena bila α semakin kecil maka nilai b akan semakin besar. Berhubung harus dibuat keputusan menolak atau tidak menolak Ho, maka harus diputuskan untuk memilih salah satu saja yang harus diperhatikan, yaitu α atau b yang diperhatikan. Pada umumnya untuk amannya dipilih nilai α.

Selain ada yang dikenal dengan Power of the test, dikenal pula adanya level of significance (Tingkat Kemaknaan). Tingkat kemaknaan disebut dengan nilai α, merupakan peluang salah dalam menolak hipotesis nol. Dengan kata lain, nilai α merupakan batas toleransi peluang salah dalam menolak hipotesis nol. Dengan kata yang lebih sederhana, nilai α ini merupakan nilai batas maksimal kesalahan menolak Ho. Penentuan nilai  α tergantung dari tujuan dan kondisi penelitian. Nilai α yang sering digunakan antara lain 100%, 5%, dan 1%. Untuk bidang kesehatan masyarakat biasanya digunakan nilai α sebesar 5%. Sementara untuk pengujian obat-obatan digunakan batas toleransi kesalahan yang lebih kecil yaitu 1% karena mengandung risiko yang fatal.

Pengujian hipotesis sangat berhubungan dengan distribusi data populasi yang akan diuji. Bila distribusi data populasi yang akan diuji berbentuk normal/simetris/Gauss, proses pengujiaan dapat digunakan dengan pendekatan uji statistik parametrik. Sementara bila distribusi data populasinya tidak normal atau tidak diketahui distribusinya, dapat digunakan pendekatan uji statistik nonparametrik.

Kenormalan suatu data dapat dilihat dari jenis variabelnya, jika variabelnya berjenis numerik/kuantitatif biasanya distribusi datanya mendekati normal/simetris. Bila jenis variabelnya kategori (kualitatif), bentuk distribusinya tidak normal sehingga menggunakan uji nonparametrik. Penentuan jenis uji juga dapat ditentukan oleh jumlah data yang dianalisis, bila jumlah data kecil yaitu kurang dari 30 maka cenderung digunakan uji nonparametrik karena untuk mendapatkan distribusi normal biasanya harus lebih sama dengan 30 jumlah datanya. 

Dalam melakukan pengujian hipotesis, terdapat tahapan-tahapannya, yaitu sebagai berikut:

1. Menetapkan hipotesis
2. Menentukan uji statistik yang sesuai
3. Menentukan batas atau tingkat kemaknaan (level of significance)
4. Menghitung menggunakan uji statistik
5. Memutuskan hasil perhitungan uji statistik

Dalam menetapkan hipotesis, seperti yang sudah dijelaskan ditetapkan Ho dan Ha-nya dengan ketentuan Ho merupakan pernyataan yang menunjukkan tidak adanya perbedaan atau hubungan sementara Ha menyatakan adanya perbedaan atau hubungan. Dengan merumuskan Ha, maka bisa ditentukan uji statistiknya one tail atau two tail, untuk mengingat kembali bisa dilihat pada tabel sebelumnya. 

Uji statistik yang digunakan harus tepat dan sesuai dengan data yang diuji. Jenis uji statistik sangat bergantung pada:

1. Jenis variabel yang akan dianalisis
2. Jenis datanya apakah dependen atau independen
3. Jenis distribusinya apakah normal atau tidak

Sebagai contoh, misalnya ingin mengetahui perbedaan mean dengan uji statistik untuk mengetahui perbedaan proporsi atau persentasenya, maka dapat digunakan uji T atau uji Anova. Sementara uji untuk mengetahui perbedaan proporsi dapat digunakan uji Kai kuadrat. 

Penentuan batas atau tingkat kemaknaan atau yang disebut dengan nilai α, tergantung tujuan penleitian yang dilakukan, seperti yang disebutkan sebelumnya apakah di bidang kesehatan masyarakat atau dalam penelitian tentang obat-obatan.

Perhitungan uji statistik dilakukan sesuai dengan jenis uji statistik yang digunakan, jika menggunakan uji T, maka dilakukan perhitungan menggunakan rumus uji T. 

Keputusan uji statistik dapat ditetapkan setelah diketahui hasil perhitungan menggunakan uji statistik. Kemungkinan keputusan adalah menolak Ho atau gagal menolak Ho. Keputusan uji statistik ini dapat dicari dengan dua pendekatan yaitu pendekatan klasik dan pendekatan probabilistik. 

Pendekatan klasik digunakan untuk memutuskan Ho ditolak atau gagal ditolak dengan cara membandingkan nilai perhitungan uji statistik dengan nilai pada tabel. Nilai pada tabel dilihat sesuai dengan jenis distribusi uji yang dilakukan. Misalnya melakukan uji Z maka yang dilihat ada tabel Z. Apabila nilai perhitungan uji statistik lebih besar dibandingkan dengan nilai yang berasal dari tabel. Apabila nilai perhitugan uji statistik lebih besar dibandingkan nilai yang berasal dari tabel maka Ho ditolak, Ho ditolak aritnya ada perbedaan kejadian yang signifikan. Sementara jika nilai perhitungan uji statistik lebih kecil dari nilai yang berasal dari tabel maka Ho gagal ditolak, Ho gagal ditolak artinya tidak ada perbedaan kejadian, perbedaan yang ada hanya akibat dari faktor kebetulan (by chance).

Pendekatan probabilitstik dapat dilakukan menggunakan aplikasi seperti Epi Info, SPSS, SAS, dan lainnya. Setiap akan melakukan uji statistik maka akan ditampilkan nilai P (P value). Dengan nilai P ini kita dapat menggunakan untuk keputusan uji statistik dengan cara membandingkannya dengan nilai α. Ketentuannya, bila nilai P £ nilai α, keputusannya Ho ditolak, sementara bila nilai P > nilai α, keputusannya Ho gagal ditolak. 

Kembali untuk diperhatikan, bahwa nilai P pada two tail adalah dua kali nilai P pada one tail. Pendekatan probabilistik ini sekarang sudah mulai digunakan oleh para ahli statistik dalam pengambilan keputusan uji statistik. 

Nilai P merupakan nilai yang menunjukkan besarnya peluang salah menolak Ho dari data penelitian. Nilai P diartikan pula sebagai nilai  besarnya peluang hasil penelitian terjadi karena faktor kebetulan (by chance). Harapannya, nilai P adalah sekecil mungkin. Dengan kata lain, kalau nilai P-nya kecil, perbedaan yagn ada pada penelitian terjadi bukan karena faktor kebetulan.